http://www.ozvalveamps.org/modulation.html | Created: 21/1/06 | Last update:
12:35 7/06/11
<<< OzValveAmps
|
Modulation
Contains:
In electronics there are two very different kinds of signal “mixing”, and this causes some confusion.
Perhaps the best known is the mixing of signals that takes place in an audio mixing desk. In this case the signals are added and have no influence over each other. They do not interact and each signal is unmodified by the other.
Less well known is the mixing of signals used in radio, and that produces many of our effects such as tremolo, vibrato, and ring mixing.
In these cases the signals are multiplied together rather than just added, and some rather strange things happen as a result.
If two signals are passing through a system such as an amplifier which is linear neither will interact with the other, but if the system is not linear, the lower frequency signal can modulate the higher by dynamically altering the transfer function or gain of the amplifier.
This alteration is called modulation or in audio intermodulation distortion.
Amplitude Modulation
This is a 1kHz sinewave modulated to 100% depth by 10Hz tremolo.

When an effect such as tremolo is desired it is necessary to seriously change the amplitude of the signal passing through in sympathy with the low frequency tremolo oscillator, but the oscillator signal itself is not desirable in the output as it causes useless and possibly damaging speaker “pumping” at the tremolo rate.
The simplest such amplitude modulator is the humble Cadmium Sulfide Light Dependent Resistor, CdS LDR, and lamp or LED, but there are also methods using the non-linear characteristics of active devices such as valves and transistors. Some devices such as the pentagrid valve and dual-gate FET are particularly suited to multiplicative mixing, that is modulating one signal by another.
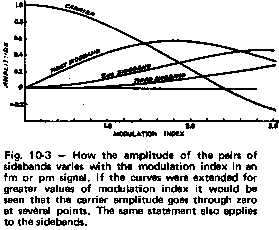
Whenever a sinewave departs from its pure monotonic sine form, such as when it is modulated and required to change amplitude or period, sidebands are formed.
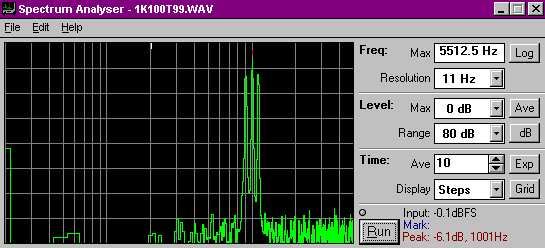
This spectrum shows the classic AM form of a stable central signal, also called the carrier, at 1 kHz with stable sidebands spaced either side by the modulating frequency.
(In this case the modulating frequency is 100Hz to better show what is happening. At 10Hz the sidebands are still there but they are too close to the carrier to be resolved with this particular spectrum analyser).
Phase Modulation
Phase modulation is often misunderstood when applied to audio frequencies, possibly due to the action of phasing effect stomp boxes. These not only shift the phase of the signal, they also add the direct signal and phase shifted signal together and thus cause frequency selective cancellation to occur at the output.
Simple phase shift alone does not produce these cancellations.
But while the phase of the wave is changing, that is actually advancing or retarding, the frequency or pitch of the signal is shifted up or down in proportion to the rate of change of the phase. In other words you can't change the phase or frequency alone - they are different views of the same thing.
If the modulating signal is a sinewave, as it normally would be in a vibrato circuit, then the change of pitch is also sinusoidal and the resulting wave effectively frequency modulated, that is, pitch-shifted.
This signal is modulated +/- one whole cycle, or 360 degrees, at a 10Hz vibrato rate.

This can be seen in the constant amplitude signal that is bunched and stretched by the modulation.
Again any change in the signal from the ideal sine form causes sidebands to be generated but, as might be expected from the oscillogram, the spectrum of this wave is significantly different to the AM case above.
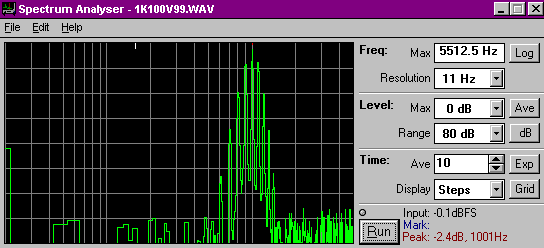
In this case there is still a strong carrier at 1kHz but it is now surrounded by a comb of sidebands, all at 100Hz spacing. While the sideband spacing is still determined by the modulating frequency, the disposition of these sidebands is determined by the modulation depth, or amount of phase shift.
If you want to dig deeper, the position and amplitude of these sidebands are determined by using Bessel functions.
Balanced Modulation
In the modulators above, in the absence of modulation the signal passes through unaltered.
In a balanced modulator, such as a ring modulator, the signal can only pass to the output when the modulator is unbalanced by the modulating signal. Without modulation no signal gets to the output.
This modulator causes a form of amplitude modulation due to cancellation, but it's also a phase modulator as it inverts the phase of the output when the modulation crosses zero.

This envelope is different again to AM and PM/FM shown above.
Again because the output signal wave is changing, sidebands are produced. But in this case the central carrier signal is cancelled out, leaving only pairs of sidebands either side of where the carrier would otherwise be (blue cursor).
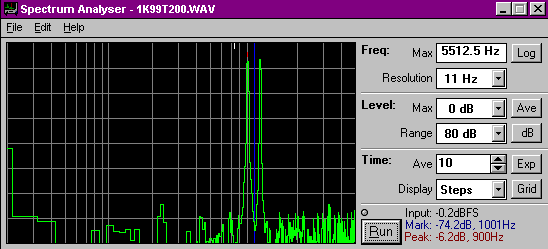
This sort of modulation is called Double Sideband Suppressed Carrier or DSBSC, is obtained from a balanced modulator such as a ring mixer, and is the general form used in some early Fender and Vox AC30 amplifiers.
This has caused an endless debate over whether this type of circuit pitch-shifts or not. This turns out to be a tricky question to answer.
The circuit does amplitude modulate due to cancellation, but this AM differs from conventional AM in that the envelope is not a sinewave like the oscillator, but is the rectified form at twice the speed.
The other point is the 180° rotation at the zero-crossing cusp. At this point the phase reverses instantly. As noted above the frequency shift in a phase modulator is proportional to the rate of change of the phase.
In this case the rate of change is very large over a very short time. In the ideal case the change is instantanious so the frequency shift is infinite, but takes place in zero time. I am indebted to Jim LeSurf for pointing out that this is a “pathological case”, and will leave it to the reader to decide if this amounts to a “yes” or “no” on the question.
Modulation samples
Below are some short sound samples of 1kHz modulated by amplitude or phase at various rates and modulation depths.
It's a commonly held view that the human ear is insensitive to signal phase, and while this is generally true for a fixed phase displacement, it is often over-simplified to the statement “you can't hear phase shift”.
This is a somewhat curious assertion given that the ear is very sensitive to pitch, and changing phase is actually frequency (pitch) modulation.
As a keyboardist (and occasional piano tuner) I know that only a few cents (hundredths of a semitone) off tune is audible and that 10 cents, a tenth of a semitone, sounds as sour as a lemon.
Far from claiming to have Golden Ears, my own hearing is a long way from perfect after years of industrial noise and working with bands, yet I have little trouble detecting a mere quarter of a cycle shift at a rate of only two cycles per second (Leslie slow).
But you don't have to take my word for it because you can audition these samples yourself. At low vibrato speeds and depths the effect is not obvious, but still detectable.
All 1 Second, *.WAV format, Mono, 11025 samples/sec, 11kb. 100Hz vibrato is musically unrealistic but expands the basic spectra to make them more easily visible.
Leslie
Since the Leslie speaker produces Doppler frequency shifting due to the tangential speed of the horn mouth the degree of frequency shift is related to the speed of the vibrato, being low at low speeds (Leslie slow) and rising with increasing modulation frequency.
But even at slow vibrato speeds and low shift (30% or 108 degrees) the shift is apparent to careful listening.
Electronic phase shifters have no problem producing large shifts at slow vibrato rates, but for a mechanical Leslie horn to produce 150% shift at a 2Hz rate by Doppler shift it would need to be about thirty feet (10m) in diameter.
At the higher vibrato speed of 10Hz, even for only 90 degree shift, the effect is more obvious (AC30). This is because the shift in frequency is not only a function of total available phase shift, but also how quickly that shift is made.
As the vibrato rate rises the phase shift becomes more rapid and the amount of frequency shift increases.
![]()